Important Questions & Solutions For Class 9 Maths Chapter 11 (Constructions)
Q.1: Construct an equilateral triangle, given its side and justify the construction.
Solution:
Construction Procedure:
- Let draw a line segment AB=4 cm .
- With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.
- With D and E as centres, draw the arcs that intersect the previous arc respectively that forms an angle of 60° each.
- Now, draw the lines from A and B that are extended to meet each other at point C.
- Therefore, ABC is the required triangle.
Justification:
From construction, it is observed that
AB = 4 cm, ∠A = 60° and ∠B = 60°
We know that, the sum of the interior angles of a triangle is equal to 180°
∠A + ∠B + ∠C = 180°
SuBstitute the values
⇒ 60° + 60° + ∠C = 180°
⇒ 120° + ∠C = 180°
⇒ ∠C = 60°
While measuring the sides, we get
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm
∠A = ∠B = ∠C = 60°
Hence, justified.
Q.2: Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment of base BC = 7 cm
- Measure and draw ∠B = 75° and draw the ray BX
- Take a compass and measure AB + AC = 13 cm.
- With B as a centre and draw an arc at the point be D
- Join DC
- Now draw the perpendicular bisector of the line BD and the intersection point is taken as A.
- Now join AC
- Therefore, ABC is the required triangle.
Q.3: Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment AB which is equal to XY + YZ + ZX = 11 cm.
- Make an angle ∠Y = 30° from point A and the angle be ∠LAB
- Make an angle ∠Z = 90° from point B and the angle be ∠MAB
- Bisect ∠LAB and ∠MAB at point X.
- Now take the perpendicular bisector of the line XA and XB and the intersection point be Y and Z respectively.
- Join XY and XZ
- Therefore, XYZ is the required triangle
Q.4: Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB – AC = 3.5 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment of base BC = 8 cm
- Measure and draw ∠B = 45° and draw the ray BX
- Take a compass and measure AB – AC = 3.5 cm.
- With B as centre and draw an arc at the point be D on the ray BX
- Join DC
- Now draw the perpendicular bisector of the line CD and the intersection point is taken as A.
- Now join AC
- Therefore, ABC is the required triangle.
Q.5: Draw a line segment AB of 4 cm in length. Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?
Solution:
According to the question,
A line segment AB of length 4cm.
To draw a perpendicular to AB through A and B, respectively.
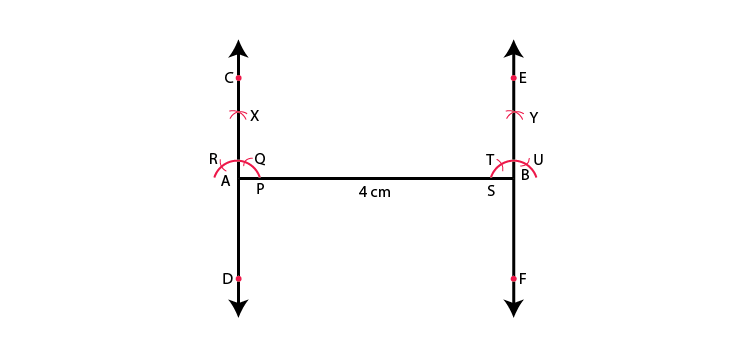
Steps of construction:
1. Draw AB = 4 cm.
2. With A as centre, draw an arc, intersecting AB at P.
3. With P as centre and the same radius, draw an arc intersecting the arc drawn in step 2 at Q.
4. With Q as centre and the same radius, draw an arc, intersecting the arc drawn in step 3 at R.
5. With R as centre and the same radius, draw an arc, intersecting the arc drawn in step 5 at X.
6. Draw OX and produced it to C and D.
7. Now, repeat the steps from 2 to 7 to draw the line EF perpendicular through B.
Yes, these lines are parallel because the sum of the interior angles on the same side of the transversal is 180 degrees.









